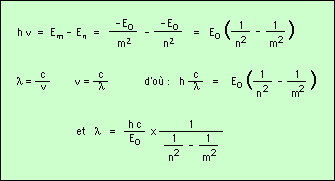Bienvenue sur le site d'astronomie de Romain Pittin.
Spectroscopie Partie théorique
6. L'atome d'hydrogène.
L’atome de Bhor
Niels Bhor a étudié le spectre de l’hydrogène, qui présente les raies apparemment les plus régulières. Il en a déduit un modèle de l’atome d’hydrogène, connu sous le nom d’atome de Bhor. Ce modèle s’inscrit dans la Mécanique Classique, et doit être abandonné maintenant au profit d’un modèle compatible avec la Mécanique Quantique. Mais il possède des propriétés didactiques assez intéressantes pour qu’on l’étudie en première approximation. Il a d’ailleurs permi des découvertes, comme celle du Deutérium, ainsi que les séries de raies hors du visible.
On note E l’énergie du photon ; ν sa fréquence (qui correspond à son énergie, donc à sa couleur) ; h est une constante nommée constante de Planck. L’énergie du photon est donnée par :
E = h ν loi de Planck
Lorsque l’électron retombe, il émet un photon dont la longueur d’onde (la couleur) est déterminée par les positions des deux orbites. Chaque couple d’orbites donne donc une raie différente de toutes les autres.
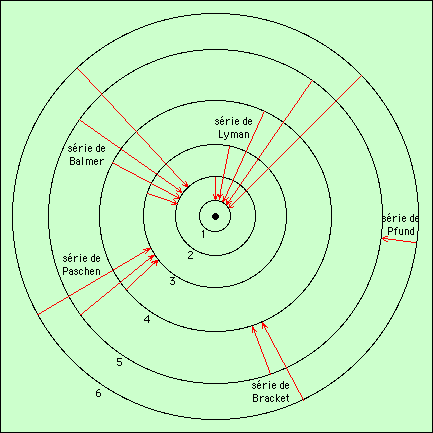
Pour l’atome d’hydrogène, on considère les séries de raies, déterminées par l’orbite sur laquelle l’électron retombe. Les six premières orbites donnent les séries suivantes :
- série de Lyman ..........niveau 1
- série de Balmer.........niveau 2
- série de Paschen.......niveau 3
- série de Bracket.......niveau 4
- série de Pfund............niveau 5.
- série de Humphreys..niveau 6
Ce schéma est indicatif, les distances entre les différentes orbites ne sont pas respectées.
Il existe une infinité de niveaux d’énergie dans chaque série, et il existe une infinité de séries. Balmer a étudié la série des raies de l’hydrogène dans le visible (depuis nommée série de Balmer), et a obtenu empiriquement la formule : ν = R0 (1/4 - 1/m2) (m > 2). Le niveau de base de la série de Balmer étant n = 2, on voit que la formule s’écrit : ν = R0 (1/n2 - 1/m2) (m > n). Elle a été vérifiée avec une excellente précision pour les autres séries, dont le niveau de base est n.
Balmer a trouvé la formule avec 1/4. On a vite généralisé en remplaçant 1/4 par 1/22, puis par 1/n2. Alors, il devint évident qu’il devait y avoir aussi des séries de raies pour n = 1, n = 3… C’est ainsi que Lymann a observé la série qui porte son nom dans l’UV (après avoir calculé la position théorique des raies) ; puis la même démarche a été suivie par Paschen dans l’infrarouge…
Calcul des orbites.
A chaque orbite correspond une énergie de liaison de l’électron. L’énergie correspondant à l’orbite n est donnée par:
où E0 est une constante, caractéristique de l’élément considéré. L’énergie du niveau 1 est donc -E0 (n=1) ; l’énergie du niveau 2 est -E0 / 4 (n=2) ; celle du niveau 3, -E0 / 9. On voit donc que cette énergie diminue très rapidement lorsqu’on s’éloigne du noyau.
L’énergie n’est pas définie de façon absolue, mais seulement relative. On ne peut définir que des variations d’énergie. Aussi, pour fixer une valeur, le choix est arbiraire. On décide alors de fixer à 0 l’énergie de liaison de l’électron, lorsqu’il est totalement libre du noyau, c’est-à-dire lorsqu’il est renvoyé à l’infini (influence du noyau nulle). Avec ce choix, l’énergie E0 vaut -13,6 eV. Elle est forcément négative. La formule se simplifie en En = -13,6 eV / n2. On peut faire le tableau des premières valeurs :
n........énergie (eV)
1.............-13,6
2.............-3,4
3..............-1,5
4.............-0,85
5.............-0,54
6.............-0,38
7.............-0,28
8.............-0,21
En tombant de l’orbite m à l’orbite n, l’électron émet un photon dont l’énergie correspond à la différence d’énergie Em - En entre les deux niveaux Em et En ; sa fréquence n est telle que :
On définit la constante de Rydberg par le premier terme de la relation obtenue (son inverse), et on considère d’autre part l’autre terme tm,n :
Prenons le cas de la série de Balmer de l’hydrogène ; elle est caractérisée par n = 2, m > 2. Calculons tm,2 pour diverses valeurs de m :
On voit que ce terme tm,2 tend vers une limite de 0,25 lorsque m tend vers l’infini. Les raies correspondantes se déduisant de ce terme constituent une série dont les espacements sont de plus en plus faibles, jusqu’à ce qu’elles ne soient plus discernables.
On peut maintenant calculer les longueurs d’onde des différentes raies de Balmer :
Ce calcul montre que les deux premières raies sont éloignées (0,6565 - 0,4860 = 0,1705 µm entre Hα et Hβ), les deux suivantes un peu moins (0,4860 - 0,4334 = 0,0526 µm entre Hβ et Hγ), et ensuite les raies se rapprochent tellement vite, que le spectroscope ne pourra même plus les distinguer. La valeur t = 0,25 correspond à ce que l’on appelle la limite de Balmer ; la longueur d’onde précise de la limite de Balmer est λ = 0,364771 µm.
C’est exactement ce qu’on observe sur un spectre de l’hydrogène, en partie dans le visible pour la série de Balmer. La première raie est isolée, la seconde et les quelques suivantes aussi, mais elles se rapprochent de plus en plus ; puis vient une bande constituée d’un grand nombre de raies indiscernables. Mais la limite de Balmer se trouve dans l’infrarouge (toutes les raies sont dans l’infrarouge à partir de Hε). Le nombre de raies séparées dépend de la finesse du réseau utilisé.
Au-delà de la série de Balmer, on note encore de la lumière : l’énergie correspondante est alors supérieure à l’énergie d’ionisation de l’atome d’hydrogène, et la lumière est émise par un électron qui arrive de l’infini pour se recombiner à l’atome. L’énergie de l’électron est quelconque, et le spectre produit est continu. Mais cette émission faiblit rapidement en s’éloignant de la limite de Balmer.